Bien que cette question ait reçu une réponse, je voulais juste ajouter quelque chose pour ceux qui recherchent une loi de potentiomètre logarithmique idéale pour la simulation. Une correspondance entre la loi linéaire et la loi logarithmique peut être trouvée sous la forme générale:

$$ y = a \ b ^ {x} + c $$

Laissez cette fonction d'équation définir un mappage de \ $ 0 \ leq x \ leq1 \ $ à \ $ ​​0 \ leq y \ leq 1 \ $, où \ $ a \ $, \ $ b \ $ et \ $ c \ $ sont des paramètres libres pour s'adapter aux courbes souhaitées.

Ceci est une équation avec trois paramètres libres afin que nous puissions choisir trois contraintes pour dériver les valeurs des paramètres. Pour un potentiomètre idéal, lorsque l'essuie-glace est au minimum, la sortie ne doit pas être de résistance, donc \ $ y = 0 \ $ quand \ $ x = 0 \ $, et ainsi $$ 0 = a + c, \ quad c = -a $$ Alors maintenant, nous avons l'équation: $$ y = ab ^ x - a. $$ Notre deuxième objectif est d'avoir une résistance maximale lorsque l'essuie-glace est au maximum, c'est-à-dire \ $ y = 1 \ $ quand \ $ x = 1 \ $, donc $$ 1 = ab - a = a (b-1), \ quad a = \ frac {1} {b-1}. $$

Enfin, nous pouvons choisir un point médian par lequel nous voulons que la courbe passe, que je laisserai définissable par l'utilisateur comme \ $ y = y_m \ $ quand \ $ x = 0.5 \ $. Cela nous donne $$ y_m = a (\ sqrt {b} - 1) = \ frac {\ sqrt {b} - 1} {b - 1} = \ frac {1} {\ sqrt {b} +1} $$ et enfin $$ b = \ gauche (\ frac {1} {y_m} - 1 \ droite) ^ 2 $$

Cela nous donne une loi de potentiomètre logarithmique paramétrique qui peut changer la quantité de courbe. Gardez à l'esprit que lorsque \ $ y_m = 0,5 \ $, \ $ a = \ infty \ $. Vous pouvez faire une carte linéaire si vous choisissez \ $ y_m = 0,5 - 10 ^ {- 5} \ $ ou quelque chose (mais pourquoi le feriez-vous!).

Habituellement, les potentiomètres coniques audio ne sont pas logarithmiques mais une approximation par morceaux avec seulement 2 segments.

Chaque segment de la piste sera revêtu d'un matériau de résistivité différent ou aura une largeur différente des autres segments.

J'ai vu des pots coniques à enroulement métallique où le premier a une largeur qui change progressivement pour atteindre la pente variable.

Un pot linéaire peut être utilisé comme un cône de diagraphie en plaçant une résistance entre l'essuie-glace et une borne, comme indiqué dans le deuxième diagramme ( Du guide Elliot Sound Products aux potentiomètres.)

Il n'y a pas de formule pour un pot à bûches. Le mieux que vous puissiez vous attendre est que le changement de résistance par angle à l'extrémité «basse» est bien moindre que celui à l'extrémité «haute». Ce serait bien si c'était logarithmique, mais ce n'est pas le cas.

Une réponse de Kevin le souligne, l'approximation la plus courante est que la piste ait deux sections linéaires (ish) différentes. C'est moins cher à faire que d'avoir un cône continuellement variable, et moins cher que d'avoir 3 sections ou plus.

Malheureusement, l'expression «log taper» a plus de degrés de liberté que la simple résistance totale, le rapport de sensibilité de haut en bas est également nécessaire. Donc, lors de l'achat d'un pot véritablement log, je devrais spécifier un pot «2 octaves» ou un pot «3 octaves». Les fabricants et les distributeurs auraient besoin de transporter plusieurs types, en vendant moins de chacun, ce qui coûterait beaucoup plus cher. Pour une application audio, vous ne voudriez probablement pas de vrai journal de toute façon, vous voudriez vous séparer du journal à un niveau bas et descendre de manière linéaire jusqu'à zéro.

La raison pour laquelle il n'y a pas de cône logarithmique défini est qu'aucune base de clients ne se soucie suffisamment de ce que le cône est exactement pour être prêt à payer suffisamment pour que les fabricants prennent la peine de normaliser quelque chose. Les potars log sont principalement utilisés dans les appareils audio, et tant que la loi de rotation est raisonnablement `` apprivoisée '', aucun client ne se soucie vraiment que le pot délivre (disons) 20 dB par 90 degrés, ils veulent juste régler un niveau.

Fait intéressant, la BBC a été confrontée à ce problème à l'IIRC dans les années 50/60, lorsqu'elle a voulu concevoir de nouveaux équipements de studio et a découvert qu'elle ne pouvait pas obtenir des pots à bûches identiques à partir de sources différentes. Ils ont donc inventé un circuit soigné qui utilisait un pot linéaire pour obtenir des performances log (ish), mais étant un pot linéaire, il était toujours reproductible. Voyez si vous pouvez décrire simplement comment cela fonctionne et pourquoi il ne crépite pas.

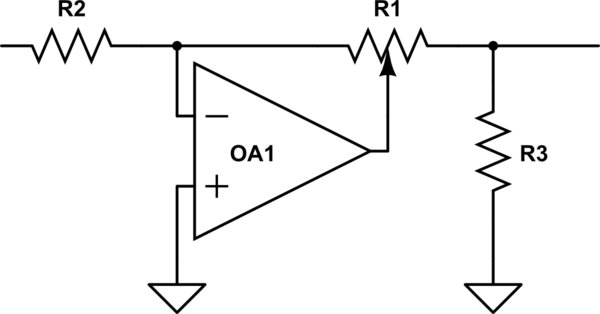
^{simuler ce circuit - Schéma créé à l'aide de CircuitLab}

Si vous configurez une expérience pour mesurer les lois du journal de votre pot, attendez-vous à ce que la loi d'un autre fabricant soit différente.

Ce schéma utilisé par la BBC m'a très bien aidé à créer un pot de bûches à partir d'un simple pot de lin dans mes projets Arduino.J'ai fait le calcul.Voici les résultats:

Soit «a» le réglage du potentiomètre (de 0 à 1).«H» est la fonction de transfert (implémentée dans le logiciel, bien sûr).

H = a / (1 + (1 - a) * K)

Avec K = 2, cela fournit une très belle approximation d'une fonction log, avec une valeur de 0,25 à «a» = 0,5.

Pour 0,1 (0,125, en fait) comme valeur à mi-chemin, ce qui suit fonctionne parfaitement:

H = a * a / (1 + (1 - a) * K);avec K = 2

J'ai utilisé un potentiomètre numérique pour agir comme un contrôle de volume audio brut.Le signal entrant va à une extrémité du pot, le signal sortant provient de l'essuie-glace et la masse commune est à l'autre extrémité.Donc si

M = Résistance totale du potentiomètre

R = Résistance entre "volume zéro" et essuie-glace

A = atténuation requise en dB

Ensuite, cela semble fonctionner assez bien:

$$ R = M \ 10 ^ {(A / 10)} $$

Comme d'autres l'ont mentionné, l'extrémité "zéro" de la course du potentiomètre sera de -∞ dB, donc à un moment donné, vous devrez abandonner la réduction linéaire des décibels.Mais au-dessus de ce point de coupure, vous voudrez peut-être que des tours de pot équivalents correspondent à des changements de décibels équivalents - peut-être 5 degrés CCW coupent 1 dB.