La réponse à votre question est NON. Avec une telle forme d'onde pour la tension (ou le courant), la réactance n'est pas définie par la même formule que celle utilisée avec les entrées et sorties état stationnaire sinusoïdal (avec ou sans modification du facteur 2 pour la fréquence) car le les concepts de réactance, d'impédance et de phaseurs s'appliquent uniquement à l ' état stationnaire sinusoïdal .

Applicabilité du concept d'impédance

Les sinusoïdes, les cosinusoïdes et leurs parents complexes, les exponentiels, ont la propriété très particulière de conserver leur forme d'onde dans des circuits linéaires invariants dans le temps. La raison de tout cela se résume à l'auto-similitude de la fonction exponentielle, mais vous pouvez penser à une explication plus `` réelle '' considérant que la dérivée d'un sinus est un cosinus (une autre fonction sinusoïdale, juste décalée) et de même, le le dérivé d'un cosinus est un sinus (ok, avec un changement de signe, il peut encore s'enregistrer comme déphasage). Et la relation constitutive des inducteurs et des condensateurs (linéaires, invariants dans le temps) est une relation linéaire impliquant des dérivés. Donc, en gros: tension ou courant sinusoïdal IN ---> courant sinusoïdal ou tension OUT.

Le seul effet qu'un circuit avec R, L et C peut avoir sur une sinusoïde est de l'atténuer et de la déphaser. On peut décrire cet effet avec une quantité mathématique qui inclut ces deux informations. Et devinez quoi, un nombre complexe fait exactement cela.

L'impédance est décrite par ce nombre complexe. Vous avez un stimulus sinusoïdal et une réponse sinusoïdale. Lorsqu'ils sont décrits par des phaseurs, leur rapport est juste un nombre complexe - l'impédance ou l'admittance selon la façon dont vous aimez le voir - décrivant à quel point la réponse a été atténuée et décalée en phase.

Inapplicabilité du concept d'impédance

MAIS toutes ces machines simplifiées ne peuvent fonctionner que si vous avez une entrée sinusoïdale et une sortie sinusoïdale. Cela ne fonctionne pas avec d'autres formes de formes d'ondes car elles sont «déformées» par des dérivés (et des intégrales). Cela signifie que lorsque vous alimentez un circuit invariant dans le temps linéaire R-L-C avec une entrée non sinusoïdale, le concept d'impédance ne peut plus être utilisé car il n'aurait aucun sens.

On peut le voir en résolvant les équations différentielles régissant le circuit ou ... en utilisant simplement un simulateur :-) J'ai couru quelques simulations LTSpice alimentant un inducteur avec une tension sinusoïdale rectifiée pleine onde et des générateurs de courant contrôlés par cette tension:

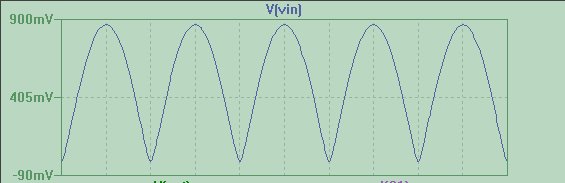
J'ai dû utiliser des générateurs de tension et de courant contrôlés en tension pour m'assurer que le circuit L ne chargeait pas le redresseur (ce qu'il fait, et beaucoup). Les résultats sont remarquablement différents.

Lorsqu'une tension V (out2) avec cette forme est forcée à travers une inductance, nous obtenons un courant qui s'accumule indéfiniment, comme le montre la forme d'onde violette I (L2). Ce n'est pas surprenant, car pour obtenir le courant, nous devons intégrer la tension dans le temps et comme V (out2) ne devient jamais négatif, nous ne pouvons qu'additionner, ajouter et ajouter ...

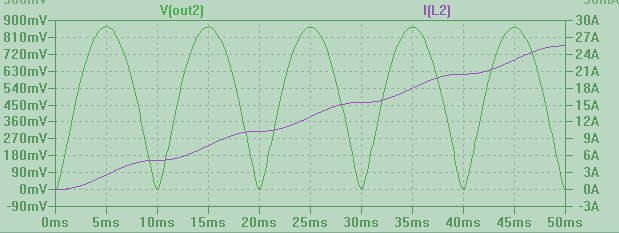
Mais si un courant I (L1) avec cette forme est forcé dans un inducteur, nous obtenons une tension triangulaire déformée périodique V (sortie) à travers celui-ci. La raison de ce comportement remarquablement différent est que maintenant, pour obtenir la forme de la tension, nous devons prendre la dérivée du courant.

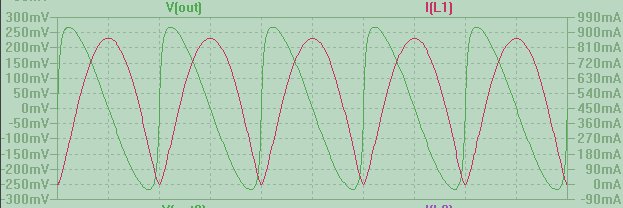
Il convient de noter que le concept d'impédance nécessite que les signaux soient both sinusoïdaux and état stationnaire . L'exemple ci-dessus a utilisé un stimulus sinusoïdal par morceaux et bien que dans chaque période la dérivée et l'intégrale soient toujours de forme sinusoïdale, la forme de forme d'onde globale ne l'est pas. Lorsque le dérivé est impliqué, nous avons des discontinuités (dans la simulation ci-dessus, elles sont adoucies parce que le signal d'entrée l'était, puisque j'ai utilisé de vraies diodes dans mon redresseur pleine onde); lorsque l'intégrale est impliquée, nous avons une accumulation due à la valeur de la constante d'intégration fixée par les conditions aux limites.

Dans les deux cas, étant donné que les dérivées et intégrales de fonctions qui ne sont pas des exponentielles, les sinus ou les cosinus retournent en général des fonctions avec une forme différente, vous ne pouvez plus décrire l'effet de l'inducteur sur la forme d'onde du stimulus comme une simple atténuation et phase décalage. L'essentiel est que vous pouvez dire adieu au concept d'impédance.

Fourier analyse à la rescousse

Vous pouvez toujours utiliser le concept d'impédance utile si vous l'appliquez dans ses limites. Si vous décomposez le signal d'entrée non sinusoïdal en une somme de sinusoïdes (même une série, ou une intégrale si elle n'est pas périodique) de fréquences différentes, vous pouvez utiliser le concept d'impédance sur chaque composante sinusoïdale unique pour trouver les composantes sinusoïdales de le signal de sortie, puis reconstruisez la forme d'onde résultante.

Bien sûr, la formule est toujours la même. Et oui, vous avez raison de dire que la fréquence fondamentale est doublée par rapport à l'onde sinusoïdale d'origine.

Ce qui est différent, c'est la façon dont la formule est utilisée. Cette formule de réactance est une représentation à fréquence unique des propriétés dépendant du temps d'un inducteur. Une sinusoïde pure n'est composée que d'une seule fréquence, vous pouvez donc facilement calculer la réactance à cette fréquence.

Une sinusoïde rectifiée est composée d'une somme infinie de sinusoïdes pures à chaque multiple entier de la fréquence fondamentale. Donc, l'équation d'origine est précise ... mais seulement pour une composante de fréquence à la fois. Techniquement, vous pouvez résoudre le circuit en calculant la réactance à chacune des composantes de fréquence (infinies), en trouvant la tension ou le courant d'intérêt et en additionnant les résultats sur toutes les fréquences, mais en fonction de l'apparence de votre circuit et des informations que vous besoin, vous pouvez choisir une approche différente pour résoudre le problème.

Pour plus d'informations, je vous recommande de rechercher la transformée de Fourier, y compris ce qu'est la transformée de Fourier d'une sinusoïde rectifiée.

Ouf!La tension d'entrée que vous avez dessinée peut être assez bien estimée avec quelques termes d'une série de Fourier.

Depuis cette page de RFCafe, une onde sinusoïdale rectifiée de 50 Hz avec une amplitude de crête de V, a ces composants:

• DC de 0,63 V
• 100 Hz de 0,42 V
• 200 Hz de 0,08 V
• 300 Hz de 0,04 V

C'est probablement suffisant pour vos besoins.

Le courant total qui circule dans une charge RL connectée à cette source est alors:

Itot = 0,63 * V / R + 0,42 * V / (sqrt (R ^ 2 + (2pi * 100 * L) ^ 2)) + ... etc

Sans R bien sûr, le courant est infini à cause du composant DC.

Après avoir montré un schéma, j'ai décidé de faire ce que Chris vous a conseillé de faire. Simulez-le numériquement.

J'ai donc choisi mon simulateur préféré, CircuitJS, et j'ai essayé de configurer le même schéma que dans votre question.

Voici ma tentative:

Lien vers la simulation pour pouvoir interagir avec elle.

• La ligne verte est la tension aux bornes de l'inductance
• La ligne jaune est le courant traversant l'inducteur
• La ligne blanche est la puissance réactive de l'inducteur

L'ampli-op le plus à gauche a l'expression mathématique suivante \ $ V_ {out} = \ text {abs ($ V_ {in} $)} \ $, l'entrée est une onde sinusoïdale avec une amplitude de 5 V. cette tension est tamponnée avec un deuxième ampli-op. Les deux amplificateurs opérationnels sont idéaux pour pouvoir fournir, en théorie, un courant infini.

L'ampli opérationnel le plus à droite agit simplement comme une source de tension idéale.

Comme vous pouvez le voir, le courant traversant l'inductance est simplement l'intégrale de la tension à travers celui-ci, qui tendra vers l'infini. La puissance réactive tendra également vers l'infini.

Lorsque la puissance réactive est connue, la réactance peut être calculée comme suit:

\ $ Q = \ frac {V ^ 2} {X} \ $

et nous voulons X

\ $ X = \ frac {V ^ 2} {Q} \ $

Donc \ $ V ^ 2 \ $ est périodique avec une amplitude qui ne changera jamais. Jamais pour toujours.

Cela signifie que \ $ X = \ frac {V ^ 2} {Q} \ $ tendra vers 0 Ω, car comme vous pouvez le voir, Q devient de plus en plus grand à l'infini (vu en blanc).

Ajout d'une simple résistance de 1 ohm en série avec l'inductance, qui évidemment devrait être là. Duh! Stupide moi.

Ensuite, vous obtenez quelque chose qui ressemble à ceci:

Voici le lien vers ce schéma si vous souhaitez interagir avec celui-ci.

Les graphiques sont identiques à ceux ci-dessus.

Derp, trop fatigué pour éditer cette question correctement. Si vous en avez envie, modifiez-le. Sinon, ne le faites pas. Adjö boys.

Non, car cette formule (\ $ X = 2 \ pi f L \ $) repose sur les propriétés des ondes sinusoïdales, et le courant alternatif rectifié n'est pas une onde sinusoïdale.

La définition de l'inductance, L, est:

$$ V = L \ frac {dI} {dt} $$

où I est le courant traversant l'inductance et V est la tension induite à travers celui-ci (avec les fonctions I et V du temps, t).

Si le courant est sinusoïdal, $$ I = \ sin (2 \ pi f t) $$ avec f la fréquence.La différenciation donne: $$ V = 2 \ pi f L \ cos (2 \ pi f t) $$

donc la forme d'onde de tension est également sinusoïdale mais avec un déphasage de 90 degrés (sin à cos) et un facteur multiplicatif de \ $ 2 \ pi f L \ $, qui est la magnitude de la réactance que vous indiquez.

Si V et / ou I ne sont pas des ondes sinusoïdales, cette relation ne tient pas.